0. 契机：

在读 accelerate 源码时，发现使用了大量的hook来解决分布式部署LLM，因此，想更加深入了解PyTorch中的hook的使用方式和原理。

1. 什么是hook？

hook（钩子）实际上在软件工程中很常见，这根本不是 PyTorch 独有的。通常，“钩子” 是在特定事件后自动执行的函数。

一些常见的hook示例：

  • 网站在您访问 N 个不同的页面后显示广告。
  • 当资金添加到您的帐户时，银行应用程序会发送通知。
  • 当环境光线变暗时，手机会调暗屏幕亮度。

当然这些示例都可以在没有hook的情况下实现。但在许多情况下，hook使程序员的生活更轻松。

2. 什么是PyTorch中的hook？

前提：为了节省在·显存（内存），PyTorch在计算过程中不保存中间变量，包括中间层的特征图和非叶子张量的梯度等。

有时对网络进行分析时需要查看或修改这些中间变量，此时就需要注册一个钩子（hook）来导出需要的中间变量。

因此：我们可以利用hook，在不改变网络输入输出的结构的前提下，方便地获取、改变网络中间层变量的值和梯度。这个功能被广泛用于可视化神经网络中间层的 feature、gradient，从而诊断神经网络中可能出现的问题，分析网络有效性。

注意：PyTorch hook是为每个 Tensor 或 nn.Module 对象触发，并由对象的向前或向后传递触发。
因此：可以将hook简单的分为：

  • Hook for Tensors ： 针对 Tensor 的 hook
  • Hook for Modules ： 针对例如 nn.Conv2dnn.Linear等网络模块的 hook

可以有如下的定义：

1
2
3
4
5
6
7
8
from torch import nn, Tensor

def module_hook(module: nn.Module, input: Tensor, output: Tensor):
    # For nn.Module objects only.
  
def tensor_hook(grad: Tensor):
    # For Tensor objects only.
    # Only executed during the *backward* pass!

值得注意的是：module_hook接收了三个参数 module 、 input 、 output 因此，每个module_hook都可以修改 input、 output 或内部 module 参数。

1. Hook for Tensor

这里只有一种func：

torch.Tensor.register_hook()

举个栗子：

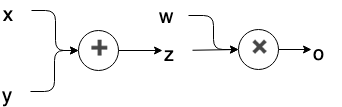
image.png

上面的计算图（computation graph）中，x y w 为叶子节点（leaf nodes），而 z 为中间变量。

在 PyTorch 的计算图中，只有叶子结点的变量会保留梯度。而所有中间变量的梯度只被用于反向传播，一旦完成反向传播，中间变量的梯度就将自动释放，从而节约内存。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import torch

x = torch.Tensor([0, 1, 2, 3]).requires_grad_()
y = torch.Tensor([4, 5, 6, 7]).requires_grad_()
w = torch.Tensor([1, 2, 3, 4]).requires_grad_()
z = x+y
# z.retain_grad()

o = w.matmul(z)
o.backward()
# o.retain_grad()

print('x.requires_grad:', x.requires_grad) # True
print('y.requires_grad:', y.requires_grad) # True
print('z.requires_grad:', z.requires_grad) # True
print('w.requires_grad:', w.requires_grad) # True
print('o.requires_grad:', o.requires_grad) # True

print('x.grad:', x.grad) # tensor([1., 2., 3., 4.])
print('y.grad:', y.grad) # tensor([1., 2., 3., 4.])
print('w.grad:', w.grad) # tensor([ 4.,  6.,  8., 10.])
print('z.grad:', z.grad) # None
print('o.grad:', o.grad) # None

由于 z 和 o 为中间变量（并非直接指定数值的变量，而是由别的变量计算得到的变量），它们虽然 requires_grad 的参数都是 True，但是反向传播后，它们的梯度并没有保存下来，而是直接删除了，因此是 None。如果想在反向传播之后保留它们的梯度，则需要特殊指定：把上面代码中的z.retain_grad() 和 o.retain_grad的注释去掉，可以得到它们对应的梯度，运行结果如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
z.retain_grad()
o.retain_grad()
----------------------------------------------------------------
output:
x.requires_grad: True
y.requires_grad: True
z.requires_grad: True
w.requires_grad: True
o.requires_grad: True
x.grad: tensor([1., 2., 3., 4.])
y.grad: tensor([1., 2., 3., 4.])
w.grad: tensor([ 4.,  6.,  8., 10.])
z.grad: tensor([1., 2., 3., 4.])
o.grad: tensor(1.)

但是，这种加 retain_grad() 的方案会增加内存占用，并不是个好办法，对此的一种替代方案，就是用 hook 保存中间变量的梯度。

对于中间变量 z，hook 的使用方式为：

z.register_hook(hook_fn)

其中 hook_fn 为一个用户自定义的函数，其签名为：

hook_fn(grad) -> Tensor or None ,其中：

  • 参数 grad:
    • 这是传递给 hook_fn 的梯度张量，即当前变量 z 在反向传播过程中计算出来的梯度。
    • 这个梯度张量的形状与变量 z 的形状一致。
  • 返回值 Tensor 或 None:
    • None: 反向传播时，梯度传播到变量 z，再继续向前传播之前，将会传入 hook_fn。如果 hook_fn的返回值是 None，那么梯度将不改变，继续向前反向传播。
    • Tensor: 如果 hook_fn 返回一个新的张量，这个张量将替代原始的梯度，并用于后续的反向传播。

值得注意的是：

  • 这里的 hook_fn 只影响tensor的反向传播，不影响推理/正向传播。
  • 注册的钩子函数只能被调用一次，即在每次反向传播过程中，只要梯度被计算，钩子函数就会被调用，但不会在未来的反向传播中重复调用，除非重新注册

下面的示例代码中 hook_fn 不改变梯度值，仅仅是打印梯度：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import torch

x = torch.Tensor([0, 1, 2, 3]).requires_grad_()
y = torch.Tensor([4, 5, 6, 7]).requires_grad_()
w = torch.Tensor([1, 2, 3, 4]).requires_grad_()
z = x+y

# ===================
def hook_fn(grad):
    print(grad)

z.register_hook(hook_fn)
# ===================

o = w.matmul(z)

print('=====Start backprop=====')
o.backward()
print('=====End backprop=====')

print('x.grad:', x.grad)
print('y.grad:', y.grad)
print('w.grad:', w.grad)
print('z.grad:', z.grad)

运行结果如下：

1
2
3
4
5
6
7
=====Start backprop=====
tensor([1., 2., 3., 4.]) # hook_fn print z.grad
=====End backprop=====
x.grad: tensor([1., 2., 3., 4.])
y.grad: tensor([1., 2., 3., 4.])
w.grad: tensor([ 4.,  6.,  8., 10.])
z.grad: None

我们发现： z绑定了 hook_fn后，梯度反向传播时将会打印出 o 对 z的偏导，和上文中 z.retain_grad()方法得到的 z 的偏导一致。

接下来可以试一下，在 hook_fn 中改变梯度值，看看会有什么结果。

1
2
3
def hook_fn(grad):
		grad = grad * 2
    print(grad)

运行结果如下：

1
2
3
4
5
6
7
=====Start backprop=====
tensor([2., 4., 6., 8.])
=====End backprop=====
x.grad: tensor([2., 4., 6., 8.])
y.grad: tensor([2., 4., 6., 8.])
w.grad: tensor([ 4.,  6.,  8., 10.])
z.grad: None

当一个变量绑定多个 hook_fn 时：

1
2
3
4
5
6
····
# ===================
z.register_hook(lambda x: 2*x)
z.register_hook(lambda x: print(x))
# ===================
····

运行结果和上面的代码相同，我们发现一个变量可以绑定多个 hook_fn，反向传播时，它们按绑定顺序依次执行。例如上面的代码中，第一个绑定的 hook_fn把 z的梯度乘以2，第二个绑定的 hook_fn打印 z的梯度。因此反向传播时，也是按照这个顺序执行的，打印出来的 z的梯度值，是其原本梯度值的两倍。

2. Hook for Module

共有三个func：

1
2
3
torch.nn.Module.register_forward_hook()
torch.nn.Module.register_backward_hook()
torch.nn.Module.register_forward_pre_hook()

难点：网络模块 module 不像 Tensor，拥有显式的变量名可以直接访问，而是被封装在神经网络中间。我们通常只能获得网络整体的输入和输出，对于夹在网络中间的模块，我们不但很难得知它输入/输出的梯度，甚至连它输入输出的数值都无法获得。除非设计网络时，在 forward 函数的返回值中包含中间 module 的输出，或者用很麻烦的办法，把网络按照 module 的名称拆分再组合，让中间层提取的 feature 暴露出来。(深有感触，这也是分布式部署LLM的难点)

为了解决这个麻烦，PyTorch 设计了两种 hook：

  • register_forward_hook
  • register_backward_hook

分别用来获取正/反向传播时，中间层模块输入和输出的 feature/gradient，大大降低了获取模型内部信息流的难度。

torch.nn.Module.register_forward_hook()

register_forward_hook的作用是获取前向传播过程中，各个网络模块的输入和输出。对于模块 module，其使用方式为： module.register_forward_hook(hook_fn) 。

其中 hook_fn的签名为：

hook_fn(module, input, output) -> None

它的输入变量分别为：模块 module，模块的输入 input，模块的输出 output 。

和对 Tensor 的 hook 不同， forward hook 不返回任何值，也就是说不能用它来修改输入或者输出的值，但借助这个 hook，我们可以方便地用预训练的神经网络提取特征，而不用改变预训练网络的结构。

举个栗子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
import torch
from torch import nn

# 首先我们定义一个模型
class Model(nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.fc1 = nn.Linear(3, 4)
        self.relu1 = nn.ReLU()
        self.fc2 = nn.Linear(4, 1)
        self.initialize()
  
    # 为了方便验证，我们将指定特殊的weight和bias
    def initialize(self):
        with torch.no_grad():
            self.fc1.weight = torch.nn.Parameter(
                torch.Tensor([[1., 2., 3.],
                              [-4., -5., -6.],
                              [7., 8., 9.],
                              [-10., -11., -12.]]))

            self.fc1.bias = torch.nn.Parameter(torch.Tensor([1.0, 2.0, 3.0, 4.0]))
            self.fc2.weight = torch.nn.Parameter(torch.Tensor([[1.0, 2.0, 3.0, 4.0]]))
            self.fc2.bias = torch.nn.Parameter(torch.Tensor([1.0]))

    def forward(self, x):
        o = self.fc1(x)
        o = self.relu1(o)
        o = self.fc2(o)
        return o

# 全局变量，用于存储中间层的 feature
total_feat_out = []
total_feat_in = []

# 定义 forward hook function
def hook_fn_forward(module, input, output):
    print(module) # 用于区分模块
    print('input', input) # 首先打印出来
    print('output', output)
    total_feat_out.append(output) # 然后分别存入全局 list 中
    total_feat_in.append(input)

model = Model()

modules = model.named_children() #
for name, module in modules:
    module.register_forward_hook(hook_fn_forward)
    # module.register_backward_hook(hook_fn_backward)

# 注意下面代码中 x 的维度，对于linear module，输入一定是大于等于二维的
# （第一维是 batch size）。在 forward hook 中看不出来，但是 backward hook 中，
# 得到的梯度完全不对。
# 有一篇 hook 的教程就是这里出了错，作者还强行解释，遗毒无穷，

x = torch.Tensor([[1.0, 1.0, 1.0]]).requires_grad_() 
o = model(x)
o.backward()

print('==========Saved inputs and outputs==========')
for idx in range(len(total_feat_in)):
    print('input: ', total_feat_in[idx])
    print('output: ', total_feat_out[idx])

运行结果为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Linear(in_features=3, out_features=4, bias=True)
input (tensor([[1., 1., 1.]], requires_grad=True),)
output tensor([[  7., -13.,  27., -29.]], grad_fn=<AddmmBackward0>)
ReLU()
input (tensor([[  7., -13.,  27., -29.]], grad_fn=<AddmmBackward0>),)
output tensor([[ 7.,  0., 27.,  0.]], grad_fn=<ReluBackward0>)
Linear(in_features=4, out_features=1, bias=True)
input (tensor([[ 7.,  0., 27.,  0.]], grad_fn=<ReluBackward0>),)
output tensor([[89.]], grad_fn=<AddmmBackward0>)
==========Saved inputs and outputs==========
input:  (tensor([[1., 1., 1.]], requires_grad=True),)
output:  tensor([[  7., -13.,  27., -29.]], grad_fn=<AddmmBackward0>)
input:  (tensor([[  7., -13.,  27., -29.]], grad_fn=<AddmmBackward0>),)
output:  tensor([[ 7.,  0., 27.,  0.]], grad_fn=<ReluBackward0>)
input:  (tensor([[ 7.,  0., 27.,  0.]], grad_fn=<ReluBackward0>),)
output:  tensor([[89.]], grad_fn=<AddmmBackward0>)

torch.nn.Module.register_backward_hook()

和 register_forward_hook相似 register_backward_hook 的作用是获取神经网络反向传播过程中，各个模块输入端和输出端的梯度值。

对于模块 module，其使用方式为：

module.register_backward_hook(hook_fn)

其中 hook_fn的函数签名为：

hook_fn(module, grad_input, grad_output) -> Tensor or None

它的输入变量分别为：模块 module，模块输入端的梯度 grad_input , 模块输出端的梯度 grad_output 。

如果模块有多个输入或者输出的话 grad_input和 grad_output可以是 tuple 类型。对于线性模块：o=W*x+b ，它的输入端包括了W、x 和 b 三部分，因此 grad_input 就是一个包含三个元素的 tuple。

这里注意和 forward hook 的不同：

1.在 forward hook 中，input 是 x，而不包括 W 和 b。

2.返回 Tensor 或者 None，backward hook 函数不能直接改变它的输入变量，但是可以返回新的 grad_input，反向传播到它上一个模块

Talk is cheap, show you the code.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
import torch
from torch import nn

class Model(nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.fc1 = nn.Linear(3, 4)
        self.relu1 = nn.ReLU()
        self.fc2 = nn.Linear(4, 1)
        self.initialize()

    def initialize(self):
        with torch.no_grad():
            self.fc1.weight = torch.nn.Parameter(
                torch.Tensor([[1., 2., 3.],
                              [-4., -5., -6.],
                              [7., 8., 9.],
                              [-10., -11., -12.]]))

            self.fc1.bias = torch.nn.Parameter(torch.Tensor([1.0, 2.0, 3.0, 4.0]))
            self.fc2.weight = torch.nn.Parameter(torch.Tensor([[1.0, 2.0, 3.0, 4.0]]))
            self.fc2.bias = torch.nn.Parameter(torch.Tensor([1.0]))

    def forward(self, x):
        o = self.fc1(x)
        o = self.relu1(o)
        o = self.fc2(o)
        return o

total_grad_out = []
total_grad_in = []

def hook_fn_backward(module, grad_input, grad_output):
    print(module) # 为了区分模块
    # 为了符合反向传播的顺序，我们先打印 grad_output
    print('grad_output', grad_output) 
    # 再打印 grad_input
    print('grad_input', grad_input)
    # 保存到全局变量
    total_grad_in.append(grad_input)
    total_grad_out.append(grad_output)

model = Model()

modules = model.named_children()
for name, module in modules:
    module.register_backward_hook(hook_fn_backward)

# 这里的 requires_grad 很重要，如果不加，backward hook
# 执行到第一层，对 x 的导数将为 None，某英文博客作者这里疏忽了
# 此外再强调一遍 x 的维度，一定不能写成 torch.Tensor([1.0, 1.0, 1.0]).requires_grad_()
# 否则 backward hook 会出问题。
x = torch.Tensor([[1.0, 1.0, 1.0]]).requires_grad_()
o = model(x)
o.backward()

print('==========Saved inputs and outputs==========')
for idx in range(len(total_grad_in)):
    print('grad output: ', total_grad_out[idx])
    print('grad input: ', total_grad_in[idx])

output:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Linear(in_features=4, out_features=1, bias=True)
grad_output (tensor([[1.]]),)
grad_input (tensor([1.]), tensor([[1., 2., 3., 4.]]), tensor([[ 7.],
        [ 0.],
        [27.],
        [ 0.]]))
ReLU()
grad_output (tensor([[1., 2., 3., 4.]]),)
grad_input (tensor([[1., 0., 3., 0.]]),)
Linear(in_features=3, out_features=4, bias=True)
grad_output (tensor([[1., 0., 3., 0.]]),)
grad_input (tensor([1., 0., 3., 0.]), tensor([[22., 26., 30.]]), tensor([[1., 0., 3., 0.],
        [1., 0., 3., 0.],
        [1., 0., 3., 0.]]))
==========Saved inputs and outputs==========
grad output:  (tensor([[1.]]),)
grad input:  (tensor([1.]), tensor([[1., 2., 3., 4.]]), tensor([[ 7.],
        [ 0.],
        [27.],
        [ 0.]]))
grad output:  (tensor([[1., 2., 3., 4.]]),)
grad input:  (tensor([[1., 0., 3., 0.]]),)
grad output:  (tensor([[1., 0., 3., 0.]]),)
grad input:  (tensor([1., 0., 3., 0.]), tensor([[22., 26., 30.]]), tensor([[1., 0., 3., 0.],
        [1., 0., 3., 0.],
        [1., 0., 3., 0.]]))

需要注意的是，对线性模块，其中 grad_input 是一个三元组，排列顺序分别为：对 bias 的导数，对输入 x 的导数，对权重 W 的导数。

注意：

register_backward_hook只能操作简单模块，而不能操作包含多个子模块的复杂模块。如果对复杂模块用了 backward hook，那么我们只能得到该模块最后一次简单操作的梯度信息。

例如：对于上面的代码稍作修改，不再遍历各个子模块，而是把 model 整体绑在一个 hook_fn_backward上：

1
2
3
....
model = Model()model.register_backward_hook(hook_fn_backward)
....

output:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Model(
  (fc1): Linear(in_features=3, out_features=4, bias=True)
  (relu1): ReLU()
  (fc2): Linear(in_features=4, out_features=1, bias=True)
)
grad_output (tensor([[1.]]),)
grad_input (tensor([1.]), tensor([[1., 2., 3., 4.]]), tensor([[ 7.],
        [ 0.],
        [27.],
        [ 0.]]))
==========Saved inputs and outputs==========
grad output:  (tensor([[1.]]),)
grad input:  (tensor([1.]), tensor([[1., 2., 3., 4.]]), tensor([[ 7.],
        [ 0.],
        [27.],
        [ 0.]]))

参考资料

https://www.cnblogs.com/sddai/p/14412250.html

https://blog.csdn.net/Brikie/article/details/114255743

https://medium.com/the-dl/how-to-use-pytorch-hooks-5041d777f904